হ্যালো বন্ধুরা, আজ আমরা একটা গুরুত্বপূর্ণ বিষয় নিয়ে কথা বলবো। অংক করতে গেলে আমাদের অনেক সময় মনে হয়, এটা তো সহজ, একটু টেকনিক ব্যবহার করলেই হয়ে যাবে। কিন্তু সত্যি বলতে, যদি ত্রিকোণমিতির সূত্র (Trigonometric Formulas) না জানি, তাহলে অংকে ভালো ফল করা অনেক কঠিন হয়ে যায়। আমি নিজেও একসময় ভাবতাম, সূত্র মুখস্ত না করে শুধু কৌশল দিয়ে কাজ চালিয়ে নেবো। কিন্তু পরে বুঝেছি, এটা শুধু নিজের জন্যই নয়, অন্যকে বোঝানোর সময়ও সমস্যা হয়। তাই আজ আমি তোমাদের সঙ্গে ত্রিকোণমিতি (Trigonometry) নিয়ে একটু বিস্তারিত আলোচনা করবো। চলো, শুরু করা যাক!
অংকের জগতে ত্রিকোণমিতি একটা বড় অংশ। ত্রিভুজের কোণ আর দৈর্ঘ্য নিয়ে কাজ করতে গেলে এর সূত্রগুলো জানা জরুরি। তুমি যদি সাইন (Sine), কোসাইন (Cosine), বা ট্যানজেন্ট (Tangent) এর মতো মৌলিক বিষয়গুলো না বোঝো, তাহলে অংকের সমস্যা সমাধান করা কঠিন হয়ে পড়ে। আবার শুধু মুখস্ত করলেও হবে না, এগুলোর মানে বুঝতে হবে। কারণ, ত্রিকোণমিতি শুধু পরীক্ষার জন্য নয়, বাস্তব জীবনেও কাজে লাগে যেমন ইঞ্জিনিয়ারিং, স্থাপত্য, এমনকি গ্রাফিক্স ডিজাইনে।
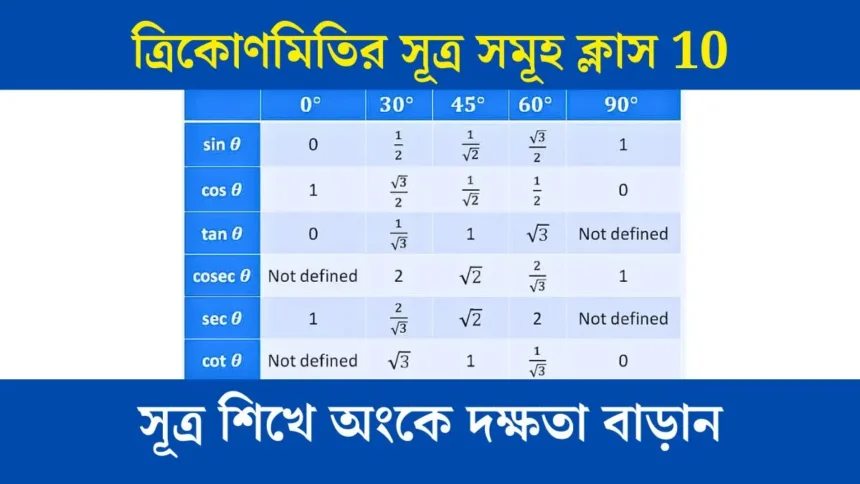
ত্রিকোণমিতির সূত্র সমূহ ক্লাস 10
ত্রিকোণমিতির সূত্রগুলো মূলত ত্রিভুজের তিনটি দিক লম্ব (Opposite), ভূমি (Adjacent), আর অতিভুজ (Hypotenuse) এর অনুপাত নিয়ে কাজ করে। চলো, একটু সহজ করে দেখি:
- সাইন (Sine): এটা হলো লম্ব আর অতিভুজের অনুপাত।
সূত্র: sin A = লম্ব / অতিভুজ
উদাহরণ: ত্রিভুজে যদি লম্ব 3 আর অতিভুজ 5 হয়, তাহলে sin A = 3/5। - কোসাইন (Cosine): এটা ভূমি আর অতিভুজের অনুপাত।
সূত্র: cos A = ভূমি / অতিভুজ
উদাহরণ: ভূমি 4 আর অতিভুজ 5 হলে, cos A = 4/5। - ট্যানজেন্ট (Tangent): এটা লম্ব আর ভূমির অনুপাত।
সূত্র: tan A = লম্ব / ভূমি
উদাহরণ: লম্ব 3 আর ভূমি 4 হলে, tan A = 3/4।
এছাড়া আরও তিনটি ফাংশন আছে, যেগুলো এদের বিপরীত। এগুলো হলো:
- কোসেকেন্ট (Cosecant): csc A = 1 / sin A = অতিভুজ / লম্ব
- সেকেন্ট (Secant): sec A = 1 / cos A = অতিভুজ / ভূমি
- কোট্যানজেন্ট (Cotangent): cot A = 1 / tan A = ভূমি / লম্ব
এই সূত্রগুলো মনে রাখা একটু কঠিন মনে হতে পারে, কিন্তু একটু চর্চা করলেই সহজ হয়ে যায়।
ত্রিকোণমিতির সূত্র সমূহ PDF
ত্রিকোণমিতির মানগুলো নির্দিষ্ট কোণের জন্য খুব গুরুত্বপূর্ণ। যেমন 0°, 30°, 45°, 90° এর মতো কোণগুলোর মান প্রায়ই পরীক্ষায় আসে।
| ফাংশন | 0° | 30° | 45° | 60° | 90° | 120° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|---|
| সাইন (Sine) | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | 0 | -1 | 0 |
| কোসাইন (Cosine) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -1 | 0 | 1 |
| ট্যানজেন্ট (Tangent) | 0 | √3/3 | 1 | √3 | অসংজ্ঞায়িত | -√3 | 0 | অসংজ্ঞায়িত | 0 |
| সেকেন্ট (Secant) | 1 | 2√3/3 | √2 | 2 | অসংজ্ঞায়িত | -2 | -1 | অসংজ্ঞায়িত | 1 |
| কোসেকেন্ট (Cosecant) | অসংজ্ঞায়িত | 2 | √2 | 2√3/3 | 1 | 2√3/3 | অসংজ্ঞায়িত | 2 | অসংজ্ঞায়িত |
| কোট্যানজেন্ট (Cotangent) | অসংজ্ঞায়িত | √3 | 1 | √3/3 | 0 | -√3/3 | অসংজ্ঞায়িত | -1 | অসংজ্ঞায়িত |
এই টেবিলটা দেখে একটু ভয় পেতে পারো, কিন্তু চিন্তা করো না। ধীরে ধীরে চর্চা করলে এগুলো মুখস্ত না করেও মনে থাকবে।
ত্রিকোণমিতির সূত্র শেখার সুবিধা ও অসুবিধা
অনেকে বলে, আমি তো টেকনিক দিয়ে অংক করি, সূত্রের দরকার কী? এটা ঠিক যে কিছু সমস্যা দ্রুত সমাধানের জন্য টেকনিক কাজে লাগে। কিন্তু যখন তুমি কাউকে পড়াতে যাবে বা জটিল সমস্যার সম্মুখীন হবে, তখন সূত্র ছাড়া অংক (Math without Formulas) করা কঠিন হয়ে যায়। আমার এক বন্ধু ছিল, ও পরীক্ষায় টেকনিক ব্যবহার করে ভালো নম্বর পেতো। কিন্তু যখন ওকে আমি বললাম, “একটা সমস্যা আমাকে বোঝা,” তখন ও হিমশিম খেয়ে গেল। কারণ, ও সূত্রের মানে বোঝেনি, শুধু কৌশল মুখস্ত করেছিল।
অন্যদিকে, সূত্র শিখলে তুমি নিজে বুঝবে এবং অন্যকেও বোঝাতে পারবে। এটা তোমার অংকের দক্ষতা (Math Skills) বাড়াতে সাহায্য করবে। তাই আমি বলবো, একটু সময় নিয়ে এই সূত্রগুলো শিখে নাও। ত্রিকোণমিতি শেখার জন্য কিছু সহজ উপায় আছে:
- চিত্র আঁকো: একটা ত্রিভুজ এঁকে তার দিকগুলো চিহ্নিত করো। এতে সূত্রগুলো বোঝা সহজ হবে।
- টেবিল মনে রাখো: উপরের টেবিলটা প্রতিদিন একটু করে দেখো। একসময় দেখবে, মুখস্ত না করেও মনে থাকছে।
- প্রশ্ন চর্চা করো: বই থেকে ত্রিকোণমিতির সমস্যা নিয়ে সমাধান করো। এতে ব্যবহারিক জ্ঞান বাড়বে।
- PDF সংগ্রহ করো: ত্রিকোণমিতির সূত্র আর মান নিয়ে অনেক ফ্রি PDF পাওয়া যায়। সেগুলো ডাউনলোড করে পড়তে পারো।
ত্রিকোণমিতি শুধু পড়াশোনার জন্য নয়, আমাদের চারপাশেও এর ব্যবহার আছে। যেমন, একটা বাড়ির ছাদের উচ্চতা মাপতে গেলে বা সূর্যের কোণ বের করতে গেলে ত্রিকোণমিতি কাজে লাগে। এমনকি গেম ডেভেলপমেন্টেও এর ব্যবহার আছে। তাই এটা শিখলে শুধু পরীক্ষায় নয়, জীবনেও কাজে আসবে।
লেখাটির শেষ কথা
বন্ধুরা, আমি আজকে ত্রিকোণমিতি নিয়ে অনেক কিছু বললাম। হয়তো প্রথমে একটু জটিল মনে হবে, কিন্তু বিশ্বাস করো, একটু চেষ্টা করলেই এটা তোমার হাতের মুঠোয় চলে আসবে। ত্রিকোণমিতির সূত্র (Trigonometric Formulas) শিখে তুমি অংকে অনেক ভালো করতে পারবে। তাই আর দেরি না করে আজ থেকেই শুরু করে দাও। কোনো সমস্যা হলে আমাকে বলতে পারো, আমি চেষ্টা করবো সহজ করে বোঝাতে। আশাকরি এই লেখাটি থেকে আপনি আপনার উত্তর পেয়েছেন এবং নোট করে নিয়েছেন। শিক্ষা সম্পর্কিত সকল তথ্য এর আপডেট পেতে শিক্ষা নিউজের এই ক্যাটাগরি ঘুরে দেখুন।